MATEMATIKA BANGUN RUAN SISI LENGKUNG

Bangun Ruang Sisi Lengkung
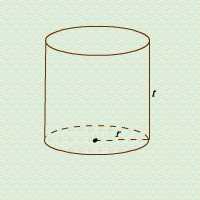
a. Tabung (Silinder )
Dalam tabung (silinder) berlaku rumus-rumus:
i. d = 2r atau r = ½ d
ii. La= Lb= πr 2 = ¼d2
iii. L s= 2πrt = πdt
iv. L p= L a+ Lb + L s= 2πr (r + t) = π d (d + t)
v. V= Lb t = L a t = π r 2 t
dengan:

r = jari-jari atas/alas tabung
d = diameter atas/ alas tabung
t= tinggi tabung
La = luas bidang atas tabung
Lb = luas bidang bawah/ alas/ dasar tabung
Ls = luas selimut/ selubung tabung
Lp= luas permukaan tabung
V = volume/ isi tabung

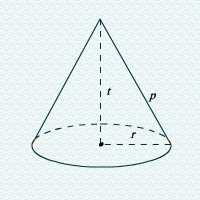
b. Kerucut
Dalam kerucut berlaku rumus-rumus:
i. d = 2r atau r = ½ d
ii. p2= t 2+ r 2
iii. Lb= πr 2 = ¼πd2
iv. L s= πrp = ½πdp
v. L p= Lb + L s= πr (r + p) =½ πd (d + p)
vi. V = π/3 r 2 t
vii. φ = r/p x 360
dengan:
r= jari-jari alas kerucut
d= diameter alas kerucut
t = tinggi kerucut
p = panjang garis pelukis atau apotema
Lb = luas bidang bawah/ alas/ dasar kerucut
Ls = luas selimut/ selubung kerucut
Lp = luas permukaan kerucut
V = volume/ isi kerucut
φ = sudut pusat rebahan
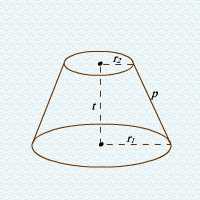
c. Kerucut Terpancung
Dalam kerucut terpancung berlaku rumus-rumus:
i. d1 = 2r1 atau r1 = ½ d 1
ii. d2 = 2r2 atau r2 = ½ d 2
iii. Lb= πr 12 = ¼ πd12
iv. La= πr 22 = ¼ πd22
v. L s= πp (r 1+ r 2)= ½πp (d1+ d2)
vi. L p= Lb + La+ L s= πp(r 1+ r 2) + π p(r 12+ r 22)
vii. V = π/3 t (r1 2+ r22 + r 1r2)
dengan:
r1 = jari-jari bidang alas/ dasar/ bawah kerucut terpancung
d1 = diameter bidang alas/ dasar/ bawah kerucut terpancung
r2 = jari-jari bidang atas kerucut terpancung
d2 = diameter bidang atas kerucut terpancung
t = tinggi kerucut terpancung
p = panjang garis pelukis atau apotema kerucut terpancung
Lb = luas bidang bawah/ alas/ dasar kerucut terpancung
La = luas bidang atas kerucut terpancung
Ls = luas selimut/ selubung kerucut terpancung
Lp = luas permukaan kerucut terpancung
V = volume/ isi kerucut terpancung
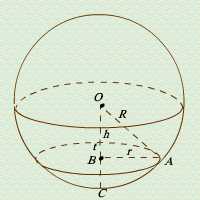
d. Bola
Dalam bola berlaku rumus-rumus:
i. D = 2R atau R= ½ D
ii. d = 2r atau r = ½ d
iii. R2 = h2+ r 2
iv. Lt = 2πRt = πDt
v. L p= 4πR 2= πD2
vi. V = 4π/ 3 R3= π/ 3D3
vii. Vt= πt2 (3R- t)
dengan:
R = jari-jari bola
D = diameter bola
r = jari-jari bidang lingkaran
d = diameter bidang lingkaran
h = jarak pusat bola ke bidang lingkaran
t = jarak dari pusat bidang lingkaran ke kulit bola
Lp = luas permukaan bola
Lt = luas bidang lengkung tembereng
V = volume/ isi bola
Vt = volume/ isi tembereng bola
2. Bangun Ruang Sisi Datar
a. Kubus
Dalam kubus berlaku rumus:
ds= a √2
dr= a √3
Lp= 6 a 2
V = a^ 3
dengan:
a = panjang rusuk kubus
ds = panjang diagonal sisi kubus
dr = panjang diagonal ruang kubus
Lp = luas permukaan kubus
V = volume/ isi kubus
b. Balok
Dalam balok berlaku rumus-rumus:
d1= √ (p2 + l2)
d2= √ (p2 + t2)
d3= √ (l2 + t2)
dr= √ (p2 + l2+ t2)
Ls= 2 (p + l )t
Lp= 2 (pl + pt + lt)
V = plt
dengan :
p = panjang balok
l = lebar balok
t = tinggi balok
d1 = panjang diagonal sisi alas/ atas
d2 = panjang diagonal sisi depan/ belakang
d3 = panjang diagonal sisi samping kiri/ kanan
dr = panjang diagonal ruang balok
Ls = luas selimut/ selubung balok
Lp = luas permukaan balok
V = volume/ isi balok
c. Prisma Tegak
Dalam prisma tegak berlaku rumus-rumus:
Luas selimut/ selubung prisma tegak = keliling alas x panjang rusuk tegak
Luas permukaan prisma tegak
Luas permukaan prisma tegak =
luas selimut + luas bidang alas + luas bidang atas
= luas selimut + 2 x luas bidang alas
= luas selimut + 2 x luas bidang atas
Volume prisma tegak= luas bidang bawah/ alas/ dasar x panjang rusuk tegak (tinggi)
= luas bidang atas x panjang rusuk tegak (tinggi)
d. Limas (Piramida)
Dalam limas (piramida) berlaku rumus-rumus:
Luas permukaan limas = luas alas + jumlah sisi tegak = luas alas + n x luas sisi tegak
Lp = Lb + n x L
Volume limas = 1/3 luas alas x tinggi
V = 1/3 Lb x t

SUMBER : http://klikbelajar.com/pelajaran-matematika/rumus-volume-dan-luas-permukaan-bangun-ruang/